Meetkunde » Oppervlakte berekenen van opgebouwde figuren
Berekenen van de oppervlakte van opgebouwde figuren gaat op de volgende manier:
| 1. | Verdeel de figuur in bekende figuren als rechthoeken en (halve) cirkels. |
| 2. | Bereken de oppervlakte van deze losse figuren. |
| 3. | Bereken de oppervlakte van de hele figuur door de oppervlakte van de losse delen bij elkaar op te tellen. |
Voorbeeld
Bereken de oppervlakte van onderstaande figuur in m2.
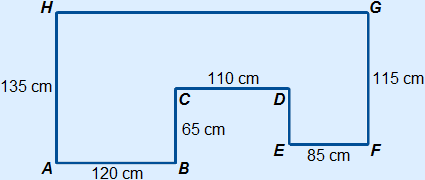
Verdeel de figuur eerst in losse delen. In dit geval drie rechthoeken.

Om de oppervlaktes te kunnen berekenen, is de lengte van CT (of DS) nodig.
CT = DS = 135 – 65 = 70 cm
Nu kunnen we alle oppervlaktes uitrekenen.
Oppervlakte rechthoek links = 120 × 135 = 16200 cm 2
Oppervlakte rechthoek midden = 110 × 70 = 7700 cm2
Oppervlakte rechthoek rechts = 85 × 115 = 9775 cm2
Oppervlakte hele figuur = 16200 + 7700 + 9775 = 33675 cm2 = 3,3675 m2
Andere manier:
De figuur kan ook op andere manieren verdeeld worden in rechthoeken.
Zie hieronder één van de andere manieren.

Deze manier zorgt echter voor meer onbekende zijden.
Nu moet eerst HT (of GS), GH (of ST) en DE (of FS) berekend worden.
HT = GS = 135 – 65 = 70 cm
GH = ST = 120 + 110 + 85 = 315 cm
DE = FS = 65 - (135 - 115) = 45 cm
Nu kunnen we alle oppervlaktes uitrekenen.
Oppervlakte rechthoek ABCT = 120 × 65 = 7800 cm 2
Oppervlakte rechthoek TSGH = 315 × 70 = 22050 cm2
Oppervlakte rechthoek EFSD = 85 × 45 = 3825 cm2
Oppervlakte hele figuur = 7800 + 22050 + 3825 = 33675 cm2 = 3,3675 m2