Handig tellen » Diagram/Rooster

Voorbeeld 1: Boomdiagram

Hoeveel mogelijkheden zijn er om met drie dobbelstenen tenminste 16 ogen te gooien.

Antwoord:
Kies steeds de mogelijkheid met het grootste aantal.
Je kunt dit met een boomdiagram systematisch doen.

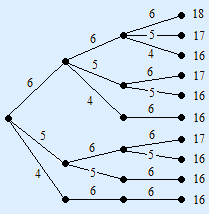
Er zijn dus 10 mogelijkheden om tenminste 16 ogen te gooien.

Voorbeeld 2: rooster/tabel

Hoeveel mogelijkheden zijn er om met twee dobbelstenen meer dan 9 ogen te gooien?

Antwoord:
Omdat het om twee dobbelstenen gaat kunnen we handig de uitkomsten van het gooien in een rooster weergeven.

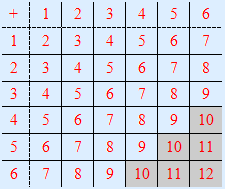
Er zijn dus 6 mogelijkheden om met 2 dobbelstenen meer dan 9 ogen te gooien.

Voorbeeld 3: Wegendiagram

Gebruik de cijfers 2, 3, 4, 5 en 6 om een getal van 4 cijfers te maken, waarbij je de cijfers vaker mag gebruiken.
Hoeveel getallen groter dan 5400 kun je maken?

Antwoord:
We gebruiken nu een wegendiagram.
Als het eerste cijfer een 5 is, moet het tweede een 4, 5, of 6 zijn en voor het derde en vierde cijfer zijn geen beperkingen.
Als het eerste cijfer een 6 is, zijn er voor het tweede, derde en vierde cijfer geen beperkingen.

	3 × 5 × 5 = 75
	5 × 5 × 5 = 125

Er zijn dus in totaal 75 + 125 = 200 getallen te maken welke groter zijn dan 5400.

Voorbeeld 4: Wegendiagram

Gebruik de cijfers 2, 3, 4, 5 en 6 om een getal van 4 cijfers te maken, waarbij je de cijfers maar één keer mag gebruiken.
Hoeveel getallen groter dan 5400 kun je maken?

Antwoord:
Als we beginnen met een 5, kan het tweede cijfer alleen een 4 of een 6 zijn.
Als het tweede cijfer een 4 is, zijn er voor het derde cijfer nog drie mogelijkheden, we hebben er immers al twee gebruikt. Datzelfde geldt voor de 6.
In beide gevallen heb je dan twee mogelijkheden voor het vierde cijfer.

Als we beginnen met een 6, zijn er voor het tweede cijfer vier, voor het derde cijfer drie en voor het vierde cijfer twee mogelijkheden.

	2 × 3 × 2 = 12
	4 × 3 × 2 = 24

Er zijn dus in totaal 12 + 24 = 36 getallen te maken welke groter zijn dan 5400.