Arithmetic » Roman, binary, octal and Babylonian numerals

Looking for an explanation about our regular numbers? Look at decimal numbers.

Contents

Roman numerals
Binary numbers
Octal numbers
Babylonian numerals
Adding in other positional systems

Roman numerals

The Roman numeral system is the most well-known system that is not a positional system. It is an additive system. The system has no symbol for zero and does not use negative numbers.

Symbol	Value	Value as a number
I	one	1
V	five	5
X	ten	10
L	fifty	50
C	one hundred	100
D	five hundred	500
M	one thousand	1000

Let us start with the list from 1 to 10:
I, II, III, IV, V, VI, VII, VIII, IX, X

The original rules were that the value of individual symbols are added unless a symbol with a lower value comes before a value with a higher value. In that case the lower value is subtracted from the higher value. V, L and D are only allowed once in a number. The numbers are written from high to low.
The following rules are added later, to get an unambiguous system:
- At most three times the same symbol in succession.
- At most one lower symbol in front of a higher symbol.
And these two rules that are not always taken in to account:
- V, L and D are not used to subtract, so not VC but XCV.
- A symbol can only be subtracted from a symbol that is five or ten times bigger, so not IC but XCIX

Examples:

Value	Roman numeral
78	LXXVIII
1244	MCCXLIV
2021	MXXI
1987	CMLXXXVIII

Exception: the number four

On clocks you often see IIII instead of IV for four. The most heard explanation is that IV were the first letters of Jupiter (IVPITER in Latin) and therefore not used. An other reason can be that IV is often upside down on a clock. It may be confused with VI. The IIII also gives a certain symmetry. IIII is as wide as VIII, which is on the other side on the clock. You then also have I, II, III, IIII (= four numerals with I), V, VI, VII, VIII (= four numerals with V) and IX, X, XI, XII (= four numerals with X).

Biggest Roman number

If you strictly uphold all rules, the biggest number possible is MMMCMXCIX = 3999, as you can only use M three times in succession.

You want bigger numbers?
On Wikipedia they explain two ways.

Binary number

The binary number system is base-2 positional numeral system.
The symbols 0 and 1 are used as digits.
Such a digit is called a bit.
A binary number with eight bits is called a byte. Therefore 8 b = 1 B.

The numbers 0 to 16 are:

Binary	Decimal
0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7
1000	8
1001	9
1010	10
1011	11
1100	12
1101	13
1110	14
1111	15
10000	16

In the decimal system 9 is incremented to 10 and 99 incremented to 100. In the binary system it also works like this, as there is only 0 and 1 a 1 is immediately incremented to 10 and 11 incremented to 100.

In the binary number, the value of each digit is a power of 2.
If necessary, compare this to the table for the decimal positional system at the top of the page.

	27	26	25	24	23	22	21	20
10011101	1	0	0	1	1	1	0	1

The binary number 10011101 is in the decimal system:
2⁷ + 2⁴ + 2³ + 2² + 2⁰ = 128 + 16 + 8 + 4 + 1 = 157

Avoid confusion

To avoid confusion you can use a subscript number to show in which number system the number is written. In our example this will look like this: 10011101₂ = 157₁₀.

Octal numbers

The octal number system is a base-8 positional numeral system.
The symbols 0 to 7 are used as digits.
In (Dutch) primary schools this numeral system is sometimes taught as: 'Het land van Oct', which translates in 'The country of Oct'. Oct is sometimes written as Okt. In the country of Oct people have eight fingers so they use the octal system.
It teaches the children abetter insight into the workings of a positional system. You cannot rely on your memory anymore, but really have to use arithmetic. For this reason the teacher is also able to recognise gaps in the thinking process with the (decimal) positional system.

The numbers 1₁₀ to 16₁₀ are in the octal system:
1, 2, 3, 4, 5, 6, 7, 10, 11, 12, 13, 14, 15, 16, 17, 20

10 is pronounced oct, 11 as oct-one, 12 as oct-two and 20 is pronounced two-oct. From 100 on it varies. In most cases 100 is a board (8×8) and 1000 a block (8×8×8). The number 5342 is pronounced five block three board four oct two.

In the decimal system 9 is incremented to 10 and 99 incremented to 100. In the octal system it also works like this. A 7 is incremented to 10, 17 to 20 and 77 to 100.

The octal number 45 has the decimal value 4 × 8 + 5 = 37.
The octal number 371 has the decimal value 3 × 64 + 7 × 8 + 1 = 249.

In the octal system, the value of each digit is a power of 8.
If necessary, compare this to the table for the decimal positional system at the top of the page.

	85	84	83	82	81	80
703 546	7	0	3	5	4	6

The number 703 546₈ is in the decimal system:
7 × 8⁵ + 0 × 8⁴ + 3 × 8³ + 5 × 8² + 4 × 8¹ + 6 × 8⁰ =
229 376 + 0 + 1536 + 320 + 32 + 6 = 231 270₁₀

Another variant is 'Het land van Zeek' (The country of Zeek). They have 6 fingers total and use a heximal (base 6) system. After 5 comes 'zeek' and after 55 comes 'azeka'. The number 352 is pronounced three zeek five azeka two.

Babylonian numerals

The Babylonian numeral system is the oldest known positional numeral system. They worked with a base-60 (sexagesimal) number system. Luckily they did not use 60 different digits, but used an additive system in which stood for 1 and for 10. These symbols come from cuneiform and are pronounced as nail and hook. They used a wedge-tipped stylus to make these in clay tablets.
Example: 23 = .

The symbols are grouped when there are more than three. Below you can see the numbers 1 to 60.

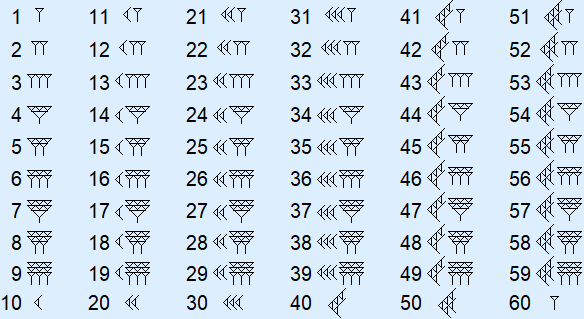
As you can see, the Babylonian numerals for 1 and 60 are the same. This is because 60₁₀ is written 10₆₀ in the sexagesimal system. However, the Babylonians had no symbol for zero. Therefore, only the was written with an (invisible) space behind it. For this reason 61 is written as two nails with a space in between. You can see this in the last example at the bottom of the page.

The number has the decimal value 60 + 25 = 85.
The number has the decimal value 13 × 60 + 46 = 826.

In the sexagesimal system, the value of each digit is a power of 60.

	603	602	601	600

is in the decimal system:
12 × 60³ + 30 × 60² + 37 × 60¹ + 55 × 60⁰ = 
2 592 000 + 108 000 + 2220 + 55 = 2 702 275

Save some time

Do you have to write a lot of Babylonian numerals?
Write a hook just as < and a nail as |.
will become

Convenient?

It looks like a very difficult number system but imagine they were used to this, just like we are used to our decimal system. The fact that angles are divided in 360° and time in 60 minutes and 60 seconds are thanks to this system. Furthermore, you will see that adding and subtracting will work the same in every positional system.
One of the possible reasons 60 was chosen is because 60 has so many divisors.
It has 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 and 60 as its divisors.

Adding in other positional systems

Let us first look at how it works in our normal decimal system. Below you see how adding works for 30 728 + 42 744 and 174 213 + 894 892.

1 1 3 0  7 2 8 4 2  7 4 4 + 7 3  4 7 2

1 1 1 1  1 7 4  2 1 3  8 9 4  8 9 2 + 1  0 6 9  1 0 5

Explanation for the left hand examaple:
Because 8 + 4 = 12 you write the 2 under the line and you have to 'carry 1' to the next digit, in this case the tens. You can write these above that column (here in red). At the hundreds you get 7 + 7 = 14. You write the 4 under the line and carry 1 to the next column, the thousands.

Adding binary numbers

Works exactly the same. Because there are only two digits, there is a higher probability you will have to carry 1.

1 1 1 0 1 0 1 0 0 1 1 1 0 0 1 1 0 0 1 + 1 1 1 0 1 1 0 0

1 1 1 1 1 1 1 0 1 1 1 0 1 1 1 0 1 1 0 1 1 0 + 1 0 1 1 1 0 0 0 1

Adding octal numbers

Works exaxtly the same. If your digit exceeds 7 you will have to carry 1.

1 1 1 5 3  7 4 0 7 2  5 6 4 + 1 4 6  5 2 4

1 1 1 2 1 7  6 0 3 3 6 7  1 3 5 + 6 0 6  7 4 0

Let us look at the left hand example. Because 4 + 6 = 12 (oct-two) you write the 2 under the line and have to carry 1 to the next column. There you get 1 + 7 + 5 = 15 (oct-five). You write the 5 under the line and carry 1. In the last column you get 5 + 7 = 14 (oct-four).

Adding Babylonian numerals

Works according to the same principal! If you exceed 9 nails you will have to carry a  and if you exceed 5 hooks you remove 6 hooks and carry a '.

Example 1

		+

First you add the number of nails in the most right hand column. There are 2 + 6 = 8 nails. Write these under the line. Proceed with the next column. Here are 3 + 4 = 7 hooks. This is one more than six, so you write down one hook under the line and carry one . In the next column you get 1 + 6 + 5 = 12 nails. You write 2 nails under the line and carry one hook. For the hooks you get 1 + 1 + 2 = 4 hooks.

Example 2

			+

First add the nails in the most right hand column. There are 4 + 7 = 11 nails. You write one nail and carry one hook to the next column. There you get 1 + 1 + 3 = 5 hooks. In the next column you have nails again. 7 + 5 = 12 nails. You write two nails and carry one hook to the next column. There you get 1 + 3 + 5 = 9 hooks. This is three more than six, so you write three hooks under the line and carry one nail. Nothing is added to this, so this will also be the result under the line.

Example 3: no zero makes for a confusing number!

			+

From right to left:
9 + 6 = 15 so write 5 nails and carry a hook.
1 + 5 + 3 = 9 so write 3 hooks (more than 6) and carry a nail.
1 + 6 + 3 = 10 so only carry a hook, as there is no symbol for zero.
1 + 4 + 1 = 6 so only carry a nail, as there is no symbol for zero.
1 + 6 + 0 = 7 so write 7 nails.
1 + 3 = 4 so write 4 hooks.

Our result      is confusing.
We mean 47 × 60² + 0 × 60 + 35 × 1 = 169 235.
However, because the zero is not there, somebody might think it means: 47 × 60 + 35 × 1 = 2855.

The Babylonians did apparently not worry to much about this, probably because from the context you could always figure out the value of a numeral. They used these numerals even as 'decimals' but had no decimal separator either! There are therefore even more possible interpretations of this Babylonian numeral.
So a by itself could mean ..., 3600, 60, 1, 1/60, 1/3600, ...
On the dots you can fill in higher powers of 60.

Placeholder

Later they came up with a placeholder for an empty space. This solved part of the problem in our result of example 3 as it would then look like this:   

However they did not use it at the end of numbers. A single nail could therefore still be 3600, 60, 1, et cetera. The placeholder is therefore not a true 'zero'.

So be thankful for the zero and the decimal separator!

To top